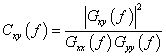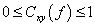- 網(wǎng)站首頁(yè)
- 關(guān)于我們
- 產(chǎn)品中心
- 技術(shù)中心
- 成功案例
- 聯(lián)系我們
- 動(dòng)態(tài)信號(hào)分析儀
- BVM-300-8(12/24)M多通道振動(dòng)測(cè)試與模態(tài)分析儀
- BVM-300-4M四通道振動(dòng)測(cè)試與模態(tài)分析儀
- BVM-300-16M振動(dòng)測(cè)試與模態(tài)分析儀
- BVM-300高速同步多通道動(dòng)態(tài)信號(hào)分析儀
- 更多
- 故障診斷類儀表
- BVM-103雙通道動(dòng)態(tài)振動(dòng)信號(hào)分析儀
- BVM-108單通道振動(dòng)數(shù)據(jù)采集器/數(shù)據(jù)分析儀
- BVM-107單通道振動(dòng)分析儀
- BVM-106巡檢儀
- BVM-300高速同步多通道動(dòng)態(tài)信號(hào)分析儀
- BVM-100-2D-J經(jīng)濟(jì)型雙通道現(xiàn)場(chǎng)動(dòng)平衡儀
- 更多
- 手持式測(cè)振表
- BVM-200測(cè)振表
- 高精度測(cè)振表
- BVM-202KT電梯振動(dòng)測(cè)試儀
- BVM-202存儲(chǔ)測(cè)振表
- BVM-200Z軸承故障診斷儀
- BVM-5936手傳振動(dòng)測(cè)試儀
- 更多
- 振動(dòng)溫度變送器
- BVM-3001多通道車載振動(dòng)監(jiān)測(cè)儀
- BVM-VT振動(dòng)溫度組合變送器
- BVM-210-9多通道振動(dòng)變送器
- BVM-DZ102電子振動(dòng)開關(guān)
- BVM-GD2風(fēng)速變送器
- BVM-232組合變送器
- 更多
- 在線監(jiān)測(cè)系統(tǒng)
- 又一款手提式在線監(jiān)測(cè)系統(tǒng)上線了
- 碼頭卸船機(jī)安全在線監(jiān)測(cè)系統(tǒng)
- 噪聲類在線監(jiān)測(cè)系統(tǒng)
- 設(shè)備在線監(jiān)測(cè)與分析系統(tǒng)
- 攀鋼與濟(jì)鋼的動(dòng)態(tài)信號(hào)采集分析系統(tǒng)
- 嵌入式平臺(tái)在線監(jiān)測(cè)及故障分析系統(tǒng)
- 更多
- 力學(xué)與結(jié)構(gòu)測(cè)試
- BVM-100-2D雙通道現(xiàn)場(chǎng)動(dòng)平衡儀/振動(dòng)數(shù)據(jù)采集器
- BVM-300-16M振動(dòng)測(cè)試與模態(tài)分析儀
- BVM-VT系列小型振動(dòng)臺(tái)
- BVM-MS系列模態(tài)激振器
- BVM-100系列配件力錘
- BVM-300-4(8/12/24)M多通道振動(dòng)測(cè)試與模態(tài)分析儀
- 更多
- 環(huán)境振動(dòng)噪聲與分析
- 噪聲測(cè)試系統(tǒng)
- BVM-300-4M四通道振動(dòng)測(cè)試與模態(tài)分析儀
- BVM-100-2S振動(dòng)噪聲采集分析儀
- HS6020聲級(jí)校準(zhǔn)器
- HS5671型精密積分聲級(jí)計(jì)
- HS6298型多功能噪聲分析儀
- 更多
- 現(xiàn)場(chǎng)服務(wù)
- 現(xiàn)場(chǎng)設(shè)備診斷服務(wù)
- 振動(dòng)狀態(tài)監(jiān)測(cè)服務(wù)
- 現(xiàn)場(chǎng)動(dòng)平衡服務(wù)
- 現(xiàn)場(chǎng)培訓(xùn)服務(wù)
- 產(chǎn)品售后技術(shù)服務(wù)
- 更多
- 技術(shù)文章
- 正弦振動(dòng)與隨機(jī)振動(dòng)狀態(tài)參數(shù)解釋
- 振動(dòng)分析儀:雙通道及四通道有什么作用?
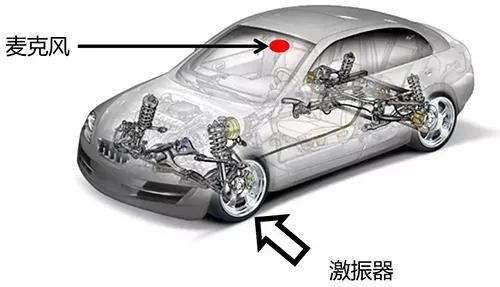
- 聲學(xué)中的相干性及其相關(guān)應(yīng)用
- 更多
- 動(dòng)平衡測(cè)試與服務(wù)成功案例
- 唐山建龍鋼鐵余熱發(fā)電鍋爐循環(huán)風(fēng)機(jī) 現(xiàn)場(chǎng)動(dòng)平衡測(cè)試報(bào)告
- 河南塔山重工機(jī)械制造有限公司動(dòng)平衡報(bào)告
- 北京航星機(jī)械制造有限公司 CT機(jī) 現(xiàn)場(chǎng)動(dòng)平衡測(cè)試報(bào)告
- 通尼科技有限公司 碎煤機(jī) 現(xiàn)場(chǎng)動(dòng)平衡測(cè)試報(bào)告
- 天津乾坤特鋼有限公司風(fēng)機(jī) 現(xiàn)場(chǎng)動(dòng)平衡測(cè)試報(bào)告
- 安德建奇立式加工中心振動(dòng)測(cè)試報(bào)告
- 更多
- 現(xiàn)場(chǎng)機(jī)械故障診斷成功案例
- 陵川金隅水泥有限公司立磨減速機(jī)故障診斷振動(dòng)測(cè)試診斷報(bào)告
- 萬(wàn)華皮帶機(jī)樓板振動(dòng)故障診斷測(cè)試報(bào)告
- 洛陽(yáng)陽(yáng)光電廠1#A、2#B鍋爐給水泵 現(xiàn)場(chǎng)動(dòng)平衡與故障診斷報(bào)告
- 比澤爾制冷技術(shù)(中國(guó))有限公司
- 與申克動(dòng)平衡儀測(cè)試對(duì)比數(shù)據(jù)
- 更多
- 模態(tài)分析成功案例
- 盤南電廠4#60萬(wàn)發(fā)電機(jī)組定子 振動(dòng)模態(tài)測(cè)試報(bào)告
- 江蘇海獅泵業(yè)制造有限公司 加氫注水泵轉(zhuǎn)子部件的模態(tài)分析與動(dòng)力學(xué)修改
- 珠海格力空調(diào)管道 振動(dòng)模態(tài)測(cè)試報(bào)告
- 更多
- 結(jié)構(gòu)力學(xué)與動(dòng)剛度測(cè)試成功案例
- 廈門諾爾起重機(jī)動(dòng)剛度測(cè)試報(bào)告
- 泵轉(zhuǎn)子部件的模態(tài)分析與動(dòng)力學(xué)改造實(shí)驗(yàn)報(bào)告
- 更多
 關(guān)于我們
關(guān)于我們
 聯(lián)系我們
聯(lián)系我們
振動(dòng)類儀器,老牌研發(fā)制造企業(yè)。國(guó)防建設(shè)的貢獻(xiàn)者。全國(guó)服務(wù)熱線:010-82895638/4168 13801221383
 中文版
中文版 ENGLISH
ENGLISH