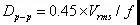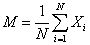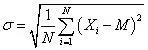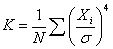91综合在线视频-91最新视频在线观看-9299yy看片黄淫大片-9299yy看片淫黄大片在线-亚洲综合免费-亚洲综合久久综合激情久久

來源：摘錄自百度文庫《附錄5 機器振動監測和分析》

各種機器的振動信號成分可以簡單地分為三類：正弦振動，隨機振動及沖擊振動。

習慣上，位移振幅單位為μm，采用峰峰值；速度振幅單位為mm/s，采用有效值；加速度振幅單位mm/s2或g，采用峰值。但也不盡然，例如，著名的GE公司對燃氣輪機出廠試驗的標準卻是以軸承座上速度值的峰值為依據的。

因為振動位移比較直觀，人們往往在測量出速度振幅后還希望折算到振動位移值，它們之間的一個簡單的換算方法是：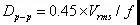

式中，Dp-p 是位移的峰峰值，Vrms 是速度幅值的均方根值，f  是正弦振動的頻率 (Hz)。例如，振動速度的均方根值等于1mm/s，則對應的位移峰峰值等于4.5μm。

實際機器的振動絕不可能是單一頻率的正弦振動。這種情況下，振動的峰值或峰峰值變得十分復雜，往往在某一個相等的短時間間隔內，它們不是一個常值，有時甚至變化很大。上式換算出來的位移振幅只是一個當量值，并不真實代表振動位移的最大值。有的機組出廠標準采用位移的真峰峰值，這種情況下，振動讀數會比按上式的標準高得多。

2. 頻率是分析振動原因的主要依據。

不同的振源引起不同頻率的振動，這也是為什么頻率分析是振動故障分析的主要方法受到特別重視的原因。對于旋轉機械的振動，根據振動頻率分為同步振動和非同步振動。同步振動的頻率是機器運行轉速的整倍數或分數，典型的同步振動有1X，2X，1/2X以及0.43X。

3. 相角實際機器振動十分復雜，討論機器上某一點振動的相角是沒有意義的。

只有單一頻率純正弦振動才有相角的概念。例如，軸振動的工頻分量（與轉速對應的頻率）與軸上某一固定標志的相位差，轉子“高點”就是基于相角測量。所謂“高點”是軸上的某一點（方向），當該點轉到徑向振動位移傳感器的位置時，振動正好是正峰值。通過確定轉子上高點的位置，能確定轉子平衡狀態及殘余不平衡量的位置。

4. 機器振型十分復雜，即使穩定振動，其振型也是瞬時變化的。

模態分析經過參數識別獲得的是機器的固有振型。實際機器承受一個或多個激勵頻率，是一個或多個強迫振動以及隨機噪聲的迭加。轉軸振型則有實際意義，在一定轉速下，轉軸沿軸向的振動變形就是轉子振型。對于單個轉子而言，經過某一階臨界轉速，振型發生變化；對于多跨轉子，每隔一定距離放置一組互相垂直的徑向位移傳感器，并利用基準相位信息就可以獲得轉子沿軸向的振動形狀，它有助于估計轉子與固定部件之間的間隙以及節點位置。

均值：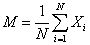

均方根值：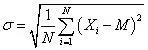

峭度 (Kurtosis)：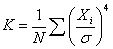

典型信號的峭度系數如下表：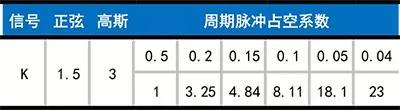

表中，d 為脈沖的占空系數，即脈沖的寬度與重復周期之比。一般運轉平衡、無明顯周期干擾的，其振動信號的幅值概率密度函數接近于正態分布。因此，峭度系數應為3左右，和振動強弱無關。